Customized Key for Container Map: Bi-match Pair of Unsigned Integers

21 Jul 2018 Languages C/C++ hash Algorithm Tree

I had a post, Container Types in C++, where I introduced a bit about one of the C++ containters std::map.
Yesterday I ran into an interesting use case of map, namely, I wanted to use map with customized key, bi-match unsigned integer pair. This post talks about the way to customize key for std::map, and issues and solution to get a bi-match unsigned integer pair work correctly as the key.

Bi-match Unsigned Integer Pair

Bi-match unsigned integer pair literally is a pair of unsigned integer (u, v), while they are regarded to be match in bi-directions.
See the following code to understand what I was targeted on:

This property could be helpful for the index of undirected edges in a graph.

Customize Key For std::map

Using customized key seems to be easy for std::map, because std::map is implemented as a template, so programmers are required to pass the type for key when declaring map objects. There is actually no issue to use normal types for key, like char, int, unsigned long and so on are all proper key types. However, if you try to use a struct, struct BimatchUIntPair for instance, as the key of map, it even cannot pass the compilation. I was so naive and thought map should get along with struct BimatchUIntPair. map wants to search whether there is a key match? Good, go ahead using operator== function. It can tell you whether keys are match, cannot it? Unfortunately, it is way wrong. Because map is implemented as red-black tree, it requires a std::less method to determine a certain order of elements, so that it can maintain the balance of the tree. By default, operator< function is used as std::less for sorting, then the logic for two objects to be deems equivalent is !(a < b) && !(b < a).

Learnt that std::less is what std::map needs, and the logic behind the scene, I proposed my first version of operator< function as follows:

But sometimes you want objects to be usable as map keys, but you do not actually have any meaningful comparison sementics, and so you don’t want to confuse people by providing operator< on your class just for that.

Then here comes an alternative approach:

And a test case:

Surprisingly, the output would be like:

1
1
1
Found
Found
Not found

In the main() we keep inserting elements into the map without deleting any, then how can a key which can be found previously “disappeared” later? To diagnose, you can try to compile with the command:

g++ -std=c++11 -DDEBUG -o main.debug main.cpp

So that you will find map does not search every elements inside to match the key. It goes to a wrong path down through the tree, as illustrated by the following figure, and excludes the chance to match the key. Wrong Path

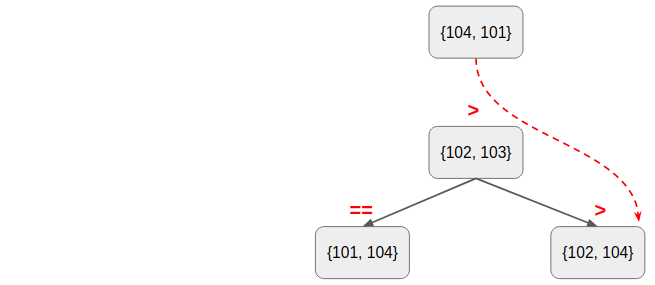
I realized then, logically my first version of the operator< function does not work. In the example, {101, 104} < {102, 103}, and {102, 103} < {104, 101}, meanwhile, {101, 104} == {104, 101}… I broke the transitive law!

Remap With Pairing Function

When I thought my goal is logically impossible, I got suggested that why not do a hash letting {104, 101} has the same hash value as {101, 104}, then use the hash value for map’s sorting? This idea solves the logic issue, while it is not easy for me to get an ideal hash function. However, thanks to Georg Cantor and Matthew Szudzik, there are pairing functions proposed by them respectively in 1878 and 2004, which fit my need.

  • Cantor pairing function Cantor Pairing Function
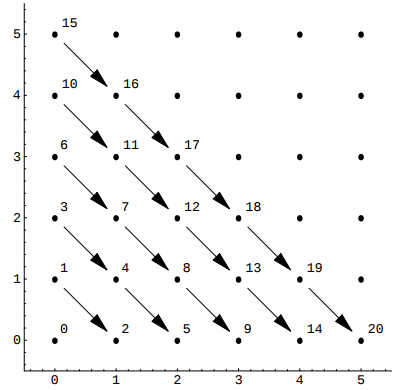
  • Szudzik pairing function Szudzik Pairing Function

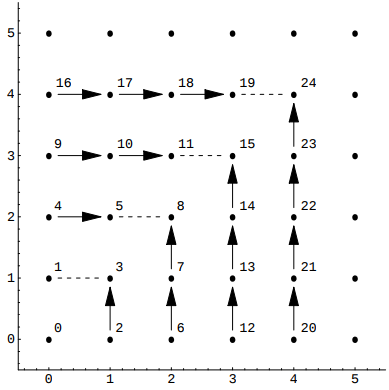
Szudzik pairing function is claimed to be more elegent, because it can take the full advantage of the range of hash value data type. In the above code, with the same return data type uint64_t, Cantor() actually only works well up to {UINT32_MAX>>1, UINT32_MAX>>1}, while Szudzik() works along with {UINT32_MAX, UINT32_MAX}.

With those pairing functions, the operator< function can be modified to behave properly for my goal.

Credits