Reuse distance calculation is a problem related to cache design and evaluation. With a sequence of address references, reuse distance is defined as the number of unique addresses between two references to the same address. For example, in “A B C A C B”, the first B has an infinite reuse distance since it has never been rereferenced, while the second B has a reuse distance of 2.

Several algorithms were discovered long time ago. The following three are included in this post:

• Stack approach - Mattson et al. in 1970;
• Bit Vector approach - Bennett & Kruskal in 1975;
• AVL Tree approach - Olken in 1981;

Stack Approach

Actually it is more like linked list than stack. Each element records both address and priority. Here come the steps to use the structure on access address A:

1. Go through the list trying to find A;
2. If there is a A found in the list, pop it out, link the privous element with the one after A, and the position number is the reuse distance of this reference, otherwise it is infinity;
3. Give A a priority, also change other elements’ priority if necessary, for LRU (Least Recent Used) strategy highest priority 0 would be assigned to A;
4. Push A to the head of the linked list, and trigger a bubble sort through the list, that either the element pushed from last slot or the element in this slot keeps go down according to whose priority is lower.

Here is an example to show the list before and after accessing to A under LRU strategy:

#	address before	priority before	bubble sort	address after	priority after
0	B	2	push B	A	0
1	C	1	push B	C	2
2	D	5	push D	B	3
3	E	0	push D	E	1
4	A	4	pop A, end	D	5
5	F	3		F	4

From the table we can know it is a reference with reuse distance of 4, because A is found in slot 4. And if this is a cache whose associativity is less than 3 ways, B would be evicted. For caches whose associativity is more than 3 and less than 5, D would be evicted. And it is a hit for all other cache having more than 5 ways per set.

Think about why a block (say F) residing outside a cache with a certain associativity (say 5-way), could have a higher priority?

Bit Vector Approach

This is suitable for LRU.

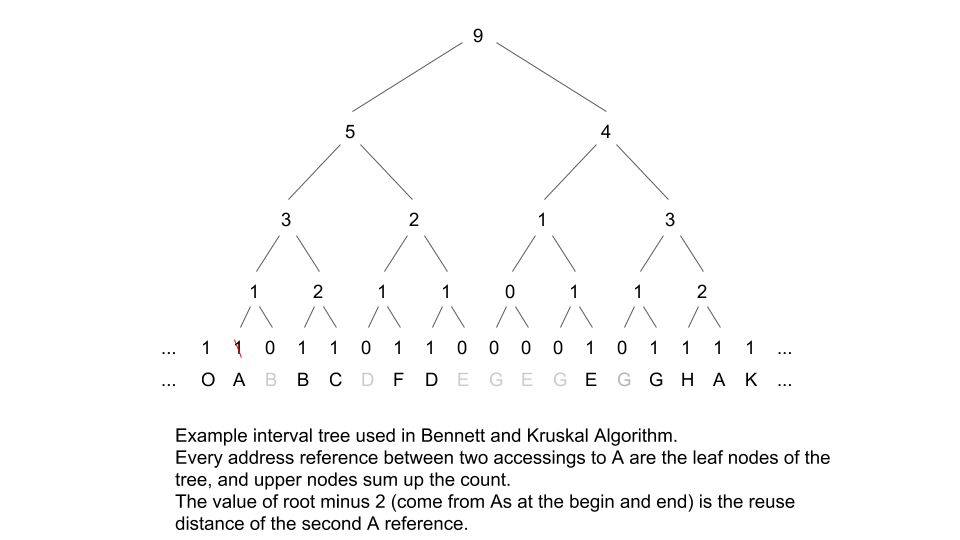
They (refer to Bennett and Kruskal) construct a bit vector as long as the address trace. Initially all the bits are set to 0. As each memory reference occurs at time t, bit b[t] is set to 1, and the bit, b[t_prev], corresponding to the time of last reference to the currently referenced page is cleard. Thus at any point t in processing the trace, all the bits are 0 except those corresponding to the most recent references of each page. We can calculate the MMC (Minimum Memory Capcity of a fully-associative cache could hit, equals to reuse distance) of a reference by counting the number of 1 bits in the interval between the current time and the last reference to the page.

To count the 1s quicker, an interval tree is maintianed as shown in the following figure.

AVL Tree Approach

Since a sequence could be mapped to a tree, why not reduce the old references to the same address, and only map the unique references in a sequence to a tree? That reduces the size of the tree to the number of unique addresses, as shown in the following figure.

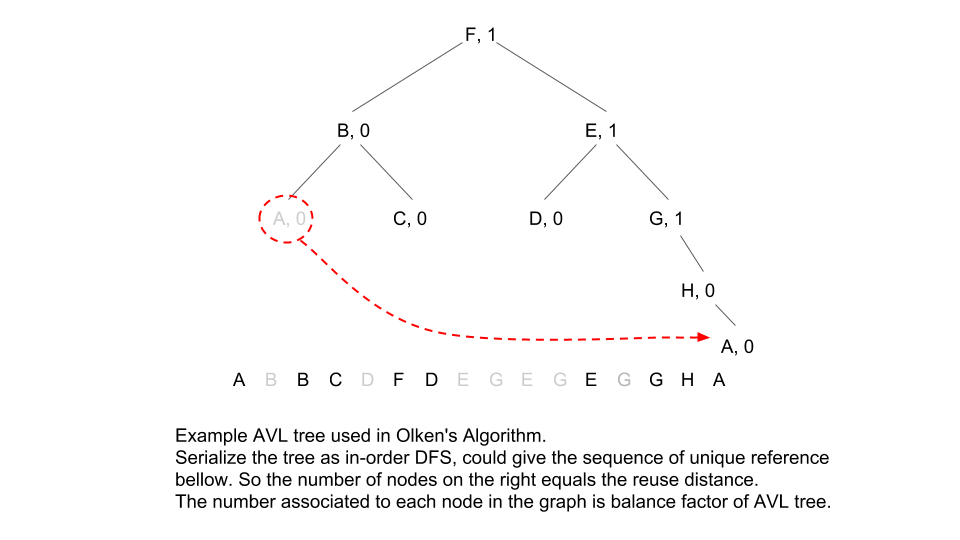
To make the operations on AVL tree more efficient, we would like to store the sum of children at each node. Here come the steps to use the structure on access address A:

1. Search the list trying to find A;
2. If there is a A found in the tree, delete it (that is copy the leftmost node in its right subtree, then delete that node), rebalance the tree, and the number of nodes on the right equals the reuse distance;
3. Insert A as the rightmost node of the tree, rebalance the tree;

Complexity Analysis

Assume the number of references is n, and there are m unique addresses, the time complexity and space usage are shown in the following table:

Algorithm	Time	Space	Coding Effort
Stack	O(nm)	O(m)	easy
Bit Vector w/ Interval Tree	O(nlog(n))	O(n)	medium
AVL Tree	O(nlog(m))	O(m)	hard

Credits

• Evaluation techniques for storage hierarchies - Paper for stack approach.
• LRU Stack Processing - Paper for bit vector approach.
• Efficient Methods for Calculating the Success Function of Fixed Space Replacement Policies - Paper for AVL tree approach, but it covers all three algorithms I learnt.